This morning I stumble across this old post, that shows how to create a recursive function with lambda. The article is very interesting and has a second part that deal with memoization. These two articles are really great ones, but I want to point out that you need really pay attention to performance each time you speak about recursion. This piece of code shows an interesting thing
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Program
{
private static Stopwatch sw = new Stopwatch();
static void TestSpeed(Func<int, int> f, int i, string msg)
{
sw.Reset();
sw.Start();
int res = f(i);
sw.Stop();
Console.WriteLine("{0,-9}{1,7} = {2,10} => {3,8:f3} ms",
msg, "(" + i + ")", res, sw.ElapsedMilliseconds);
}
public static void Main()
{
Func<int, int> fib = Extend.Y<int, int>(f => n => n > 1 ? f(n - 1) + f(n - 2) : n);
TestSpeed(fib, 37, "fib");
Func<int, int> fib2 = null;
fib2 = n => n > 1 ? fib2(n - 1) + fib2(n - 2) : n;
TestSpeed(fib2, 37, "fib2");
|
I use the Y function described in that article, so the previous code creates two functions: the first, called fib, is the real recursive one, the other, called fib2, is the standard one that is not really recursive, as explained in the first article, if we look at the output we see that fib is much more slower than fib2.
1
2
| fib (37) = 24157817 => 7807.000 ms
fib2 (37) = 24157817 => 822.000 ms
|
The reason is that the Y function creates a recursive lambda inserting an intermediate delegate into the call chain, it is clear if you modify the code in this way
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| Func<int, int> fib3 = Extend.Y<int, int>(f => n =>
{
StackTrace st = new StackTrace();
Console.Write("{0}-{1} ", n, st.FrameCount);
return n > 1 ? f(n - 1) + f(n - 2) : n;
});
TestSpeed(fib3, 5, "fib3");
Console.WriteLine();
Func<int, int> fib4 = null;
fib4 = n =>
{
StackTrace st = new StackTrace();
Console.Write("{0}-{1} ", n, st.FrameCount);
return n > 1 ? fib4(n - 1) + fib4(n - 2) : n;
};
TestSpeed(fib4, 5, "fib2");
Console.WriteLine();
|
I simply write the value of n and the frameCount of the stack, the result is
1
2
| 5-4 4-6 3-8 2-10 1-12 0-12 1-10 2-8 1-10 0-10 3-6 2-8 1-10 0-10 1-8
5-3 4-4 3-5 2-6 1-7 0-7 1-6 2-5 1-6 0-6 3-4 2-5 1-6 0-6 1-5
|
It is quite cryptic, but in the higher row you can see that the FrameCount is higher than the lower line, if instead of printing st.FrameCount you print st.ToString (the full stack) you obtain a lot of output. This is the part of the real recursive function
1
2
3
4
5
6
7
8
| [4]- at ConsoleApplication1.Program.<>c__DisplayClass6.<Main>b__1(Int32 n)
at ConsoleApplication1.Extend.<>c__DisplayClassb`2.<>c__DisplayClassd.<Y>b__a(A a)
at ConsoleApplication1.Program.<>c__DisplayClass6.<Main>b__1(Int32 n)
at ConsoleApplication1.Extend.<>c__DisplayClassb`2.<>c__DisplayClassd.<Y>b__a(A a)
at ConsoleApplication1.Program.<>c__DisplayClass6.<Main>b__1(Int32 n)
at ConsoleApplication1.Extend.<>c__DisplayClassb`2.<>c__DisplayClassd.<Y>b__a(A a)
at ConsoleApplication1.Program.TestSpeed(Func`2 f, Int32 i, String msg)
at ConsoleApplication1.Program.Main()
|
Compare it with the corresponding run of the fib4 (not real recursive lambda).
1
2
3
4
5
| [4]- at ConsoleApplication1.Program.<>c__DisplayClass4.<Main>b__2(Int32 n)
at ConsoleApplication1.Program.<>c__DisplayClass4.<Main>b__2(Int32 n)
at ConsoleApplication1.Program.<>c__DisplayClass4.<Main>b__2(Int32 n)
at ConsoleApplication1.Program.TestSpeed(Func`2 f, Int32 i, String msg)
at ConsoleApplication1.Program.Main()
|
As you can see in the first listing, for each recursion step, we have two function calls in the stack, this is due to the Y operator used to create the real recursive lambda function.
1
2
3
4
5
| public static Func<A, R> Y<A, R>(Func<Func<A, R>, Func<A, R>> f)
{
Recursive<A, R> rec = r => a => f(r(r))(a);
return rec(rec);
}
|
This function takes the original lambda and convert it into a real recursive one, but it creates another lambda that actually does the magic.
Let’s see with Reflector what happens, this is the disassembling for the fib2 (not real recursive function)
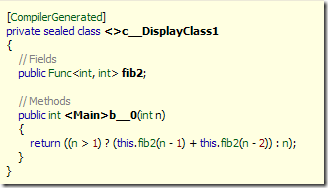
The compiler generate a class that holds the fib2 lambda and in the b__0 function it simply uses the delegate we defined. From this code you can see that the function is not really recursive, because b__0 simply invoke the fib2 delegate. A very different situation happens when we use the Y function, I let you use reflector to check generated code.
Remember also that recursion is a beautiful technique, but it is really slower than a non recursive algorithm, here is a standard implementation for the fibonacci that is not recursive.
1
2
3
4
5
6
7
8
9
10
11
12
| Func<int, int> fib3 = n =>
{
Int32 result = 1;
Int32 previous = -1;
for (Int32 num = 0; num <= n; ++num)
{
Int32 newFibNumber = result + previous;
previous = result;
result = newFibNumber;
}
return result;
};
|
Compare the timing with the recursive ones
1
2
3
| fib (37) = 24157817 => 7874.000 ms
fib2 (37) = 24157817 => 829.000 ms
fib3 (37) = 24157817 => 0.000 ms
|
The non recursive version is almost instantaneous.
alk
Tags: Lambda Lambda Recursion

